Algorithm for Bone Remodelling Using FEM
Main Article Content
Abstract
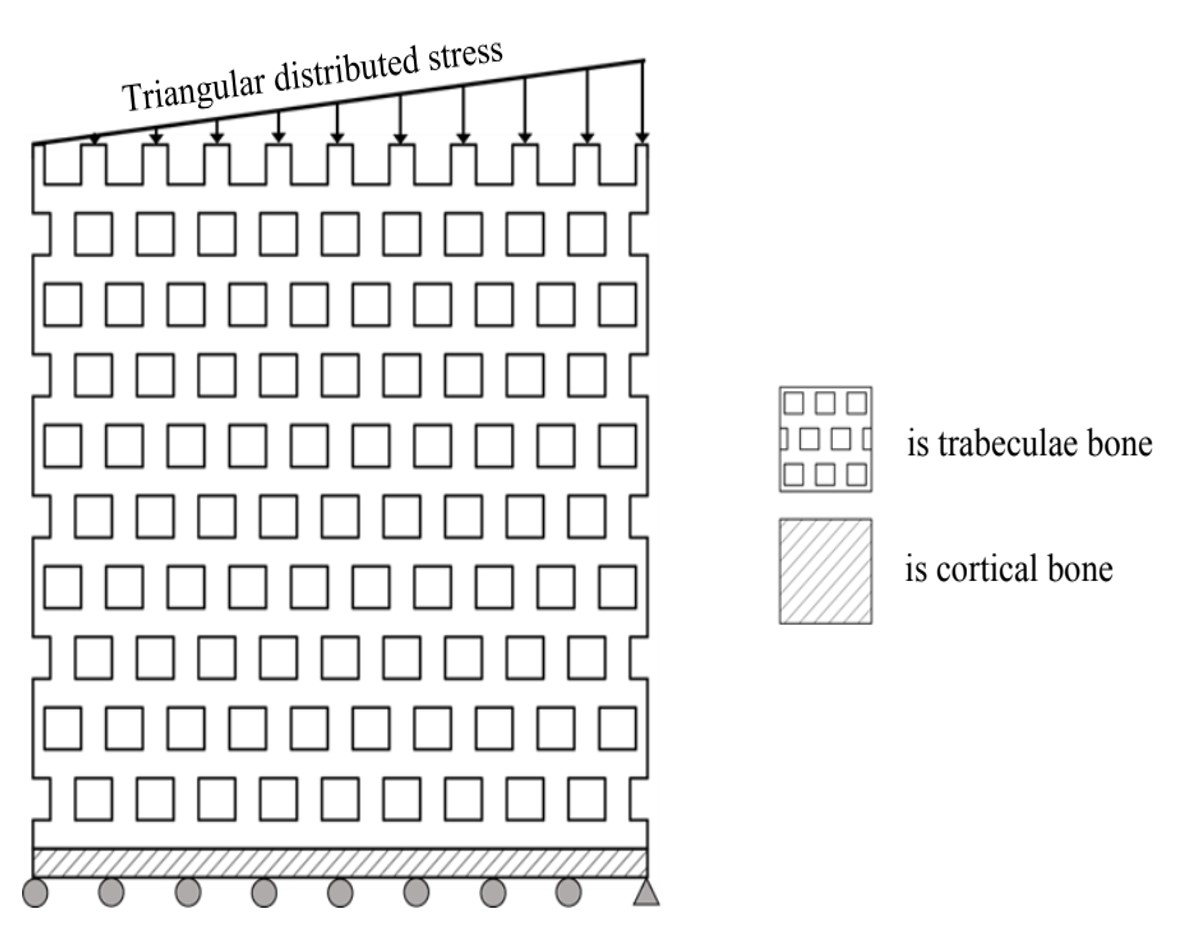
To repair the injured area and adjust strength to meet the need of the human body, resorption and formation of bones can occur throughout the lifespan depending on the strain factor. An adaptation of the trabecular bone architecture is influenced by load characteristics and outside geometry according to Wolff's law theory. In this paper, a 2D square model of trabecular bone was simulated in finite element analysis (FEA) with varying triangular distribution in compressive load, and the architecture of the trabecular bone was then altered by adding and reducing the element in the direction of the strain based on bone remodelling behavior. Finally, the FEM results showed that the trabecular bone was redesigned and adjusted to have an architecture based on load characteristics and geometry, as described by Wolff's law. This study can be used to predict the architecture and the porosity of trabecular bone.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
References
Wolff J. The law of bone remodelling. Berlin: Springer; 1986.
Eriksen EF, Gundersen HJG, Melsen F, Mosekilde L. Reconstruction of the formative site in iliac trabecular bone in 20 normal individuals employing a kinetic model for matrix and mineral apposition. Metab Bone Dis Relat Res. 1984;5(5):243-252.
Frost HM. A 2003 update of bone physiology and Wolff's law for clinicians. Angle Orthod. 2004;74(1):3-15.
Cowin SC. Bone Mechanics Handbook. 2nd ed. Boca Raton: CRC Press; 2001.
Mirulla AI, Pinelli S, Zaffagnini S, Nigrelli V, Ingrassia T, Paolo SD, et al. Numerical simulations on periprosthetic bone remodeling: a systematic review. Comput Methods Programs Biomed. 2021;204:106072.
Fernández JR, García-Aznar JM, Martínez R, Viaño JM. Numerical analysis of a strain-adaptive bone remodelling problem. Comput Methods Appl Mech Eng. 2010;199(23-24):1549-1557.
Baldonedo J, Fernández JR, Segade A. Numerical analysis of a bone remodeling model with damage. Comput Methods Appl Mech Eng. 2020;367:113113.
Jang IG, Kim IY. Computational study on the effect of loading alteration caused by disc degeneration on the trabecular architecture in human lumbar spine. J Biomech. 2010;43(3):492-499.
Park S, Park J, Kang I, Lee H, Noh G. Effects of assessing the bone remodeling process in biomechanical finite element stability evaluations of dental implants. Comput Methods Programs Biomed. 2022;221:106852.
Weinans H, Huiskes R, Grootenboer HJ. The behavior of adaptive bone-remodeling simulation models. J Biomech. 1992;25(12):1425-1441.
Mullender MG, Huiskes R, Weinans H. A physiological approach to the simulation of bone remodeling as a self-organizational control process. J Biomech. 1994;27(12):1389-1394.
Klintström E, Smedby O, Moreno R, Brismar TB. Trabecular bone structure parameters from 3D image processing of clinical multi-slice and cone-beam computed tomography data. Skeletal Radiol. 2014;43(2):197-204.
Wu D, Isaksson P, Ferguson SJ, Persson C. Young’s modulus of trabecular bone at the tissue level: a review. Acta Biomater. 2018;78:1-12.
Rho JY, Ashman RB, Turner CH. Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements. J. Biomech. 1993;26(2):111-119.