การประยุกต์ใช้ขั้นตอนวิธีของดิสตราในการกำหนดจุดหมายปลายทาง ของนักท่องเที่ยว กรณีศึกษาจังหวัดอุบลราชธานี
Main Article Content
บทคัดย่อ
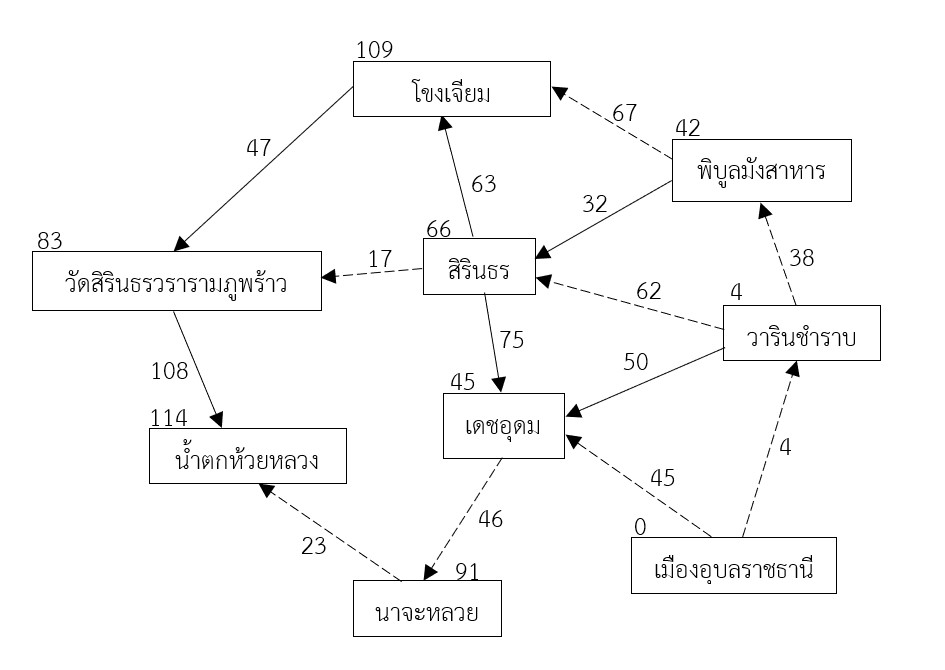
งานวิจัยนี้มีวัตถุประสงค์เพื่อศึกษาขั้นตอนวิธีของดิสตรา เพื่อหาระยะทางที่สั้นที่สุดจากต้นทาง อำเภอเมืองอุบลราชธานี ไปยังปลายทางสถานที่ท่องเที่ยว 2 แห่ง คือ วัดสิรินธรวรารามภูพร้าว และน้ำตกห้วยหลวง โดยกำหนดจุดแทน สถานที่ท่องเที่ยว และอำเภอ ซึ่งประกอบด้วย วัดสิรินธรวรารามภูพร้าว น้ำตกห้วยหลวง อำเภอวารินชำราบ อำเภอพิบูลมังสาหาร อำเภอเดชอุดม อำเภอสิรินธร อำเภอนาจะหลวย อำเภอโขงเจียม และกำหนดเส้นเชื่อมแทนระยะทางระหว่างอำเภอไปยังอำเภอ และอำเภอไปยังสถานที่ท่องเที่ยว สำหรับขั้นตอนวิธีของดิสตรา ประกอบไปด้วยการดำเนินการ 3 ขั้นตอน คือ การกำหนดค่าระยะทางให้จุด การเลือกจุดที่มีค่าระยะทางที่ดีที่สุด และการปรับแก้ค่าระยะทางของจุดให้ดีขึ้น ผลการวิจัยพบว่า การใช้ขั้นตอนวิธีของดิสตราเพื่อหาระยะทางที่สั้นที่สุดของการเดินทางจากอำเภอเมืองอุบลราชธานีถึงวัดสิรินธรวนารามภูพร้าว และจากอำเภอเมืองอุบลราชธานีถึงน้ำตกห้วยหลวงมีเส้นทางจราจรที่เป็นไปได้ทั้งหมด 2 เส้นทาง ระยะทางที่สั้นที่สุดเท่ากับ 83 กิโลเมตร และ 114 กิโลเมตร ตามลำดับ และมีเส้นทาง คือ อำเภอเมืองอุบลราชธานี - อำเภอวารินชำราบ – อำเภอสิรินธร - วัดสิรินธรวรารามภูพร้าว และอำเภอเมืองอุบลราชธานี – อำเภอวารินชำราบ – อำเภอเดชอุดม – อำเภอนาจะหลวย – น้ำตกห้วยหลวง ตามลำดับ ซึ่งทั้งสองเส้นทางมีค่าระยะทางที่สั้นที่สุดใกล้เคียงกับระบบค้นหาเส้นทางในปัจจุบัน
Article Details

อนุญาตภายใต้เงื่อนไข Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
บทความที่ได้รับการตีพิมพ์ในวารสารฯ ท้ังในรูปแบบของรูปเล่มและอิเล็กทรอนิกส์เป็นลิขสิทธิ์ของวารสารฯ
เอกสารอ้างอิง
W. Khammanee, Introduction to Graph Theory, Bangkok, Thailand: Chulalongkorn University Publisher, 2016. (in Thai)
S. Kongganuan, Kongganuan Discrete mathematics, Bangkok, Thailand: Thammasat University Publisher, 2014. (in Thai)
E. W. Dijkstra, “A note on two problems in connexion with graphs.” Numerische Mathematik. Accessed: May. 25, 2021. [Online]. Available: http://www-m3.ma.tum.de/foswiki/pub/MN0506/WebHome/dijkstra.pdf
Department of Highways, “Geographic Information System for Travel.” Department of Highways. Accessed: Jul. 6, 2021. [Online]. Available: https://dohgis.doh.go.th/dohtotravel
Google, “Google Maps.” Google. Accessed: Jul. 6, 2021. [Online]. Available: https://www.google.co.th /maps
S. Asawakulchai, “Traffic route for the shortest path travelling using Dijkstra algorithm,” Association of Private Higher Education Institutions of Thailand under the Patronage of Her Royal Highness Princess Mahachakri Sirindhorn, vol. 6, no. 1, pp. 5-14. Jun. 2017. (in Thai)
T. Suwanpruek, S. Preechaweerakul and W. Sutiwipakorn, “The development of an optimal safe path for trip planning.” Prince of Songkhla University. Accessed: Mar. 8, 2022. [Online]. Available: http://phoenix.eng.psu.ac.th/qa/Reference_EQA53/EQA_03(3)/PEC-9%20P25.pdf (in Thai)