Iterative Based Time Domain Equalization Method for DFTS-OFD in Highly Mobile Environments

Article Sidebar

PDF
DOI: https://doi.org/10.37936/ecti-cit.2017111.91711
Keywords:
DFTS-OFDM Time Domain Equalization (TDE) Channel Impulse Response (CIR) Estimation Time Domain Training Sequence (TS) Maximum Likelihood (ML) Estimation PCGS Algorithm Banded Matrix

Main Article Content

Pongsathorn Reangsuntea
Department of Electrical and Electronic Engineering, Graduate School of Engineering, Mie University, Japan
Arttapol Reangsuntea
Department of Telecommunication Engineering, Faculty of Engineering, King Mongkuts Institute of Technology Ladkrabang, Thailand
Pisit Boonsrimuang
Department of Telecommunication Engineering, Faculty of Engineering, King Mongkuts Institute of Technology Ladkrabang, Thailand
Kazuo Mori
Department of Electrical and Electronic Engineering, Graduate School of Engineering, Mie University, Japan
Hideo Kobayashi
Department of Electrical and Electronic Engineering, Graduate School of Engineering, Mie University, Japan

Abstract

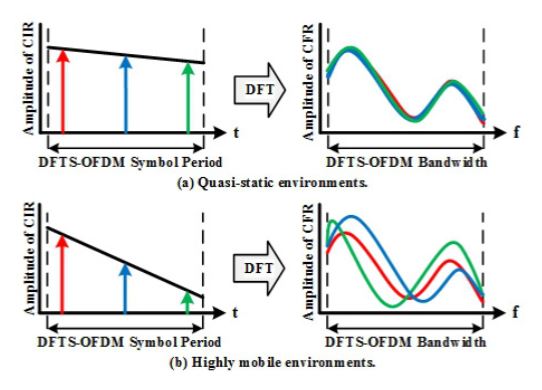
In highly mobile environments, signal quality of discrete Fourier transform spreading-orthogonal frequency division multiplexing (DFTS-OFDM) with a frequency domain equalization method would be degraded due to the occurrence of inter-channel interference (ICI). To solve this problem, this paper proposes an iterative based time domain equalization (TDE) method with a time domain channel impulse response (CIR) estimation for DFTS-OFDM signals. The salient features of the proposed method are the use of a time domain training sequence (TS) in the estimation of CIR instead the conventional pilot subcarriers and to employ the TDE method with a maximum likelihood (ML) estimation instead of the conventional one-tap minimum mean square error frequency domain equalization (One-Tap MMSE- FDE) method. This paper also proposes a low complexity iterative based TDE method using the properties of a symmetric banded CIR transfer matrix for solving the simultaneous equations instead of direct calculation of an inverse matrix. It also presents various simulation results in highly mobile environments to demonstrate the effectiveness of the proposed iterative based TDE with CIR estimation for the TS inserted DFTS-OFDM signals compared to the conventional One-Tap MMSE-FDE method.

Article Details

How to Cite
[1]
P. Reangsuntea, A. Reangsuntea, P. Boonsrimuang, K. Mori, and H. Kobayashi, “Iterative Based Time Domain Equalization Method for DFTS-OFD in Highly Mobile Environments”, ECTI-CIT Transactions, vol. 11, no. 1, pp. 28–39, Jul. 2017.
Issue
Vol. 11 No. 1 (2017): ECTI Transaction on CIT (May 2017)
Section
Artificial Intelligence and Machine Learning (AI)

References

D. Falconer, S. L. Ariyavisitakul, A. Benyamin-

Seeyar, and B. Eidson, “Frequency domain

equalization for single-carrier broadband wireless

systems,” IEEE Commun. Mag., vol. 40, pp.

-66, Apr. 2002.

N. Benvenuto and S. Tomasin, “On the comparison

between OFDM and single carrier modulation

with a DFE using a frequency-domain feed

forward filter,” IEEE Trans. Commun. Mag.,

vol. 50, pp. 947-955, Jun. 2002.

G. M. Hyung, L. Junsung, and J. G. David, “Single

carrier FDMA for uplink wireless transmission,”

IEEE Vehicular Technology. Mag., vol. 1,

no. 3, pp. 30-38, Sep. 2006.

D. Y. Seol, U. K. Kwon, and G. H. Im, “Performance

of single carrier transmission with cooperative

diversity over fast fading channels,” IEEE

Trans. Commun., vol. 57, no. 9, pp. 2799-2807,

Sep. 2009.

A. Ghosh, R. Ratasuk, B. Mondal, N. Mangalvedhe,

and T. Thomas, “LTE-advanced:

next-generation wireless broadband technology,”

IEEE Wireless Commun., vol. 17, no. 3, pp. 10-

, Jun. 2010.

3GPP TS 36.211, Evolved Universal Terrestrial

Radio Access (EUTRA); Physical Channels and

Modulation, 3GPP Standard, Rev. 10.0.0, 2011.

L. Yang, G. Ren, B. Yang, and Z. Qiu, “Fast

Time-Varying Channel Estimation Technique for

LTE Uplink in HST Environment,” IEEE Trans.

Vehicular Technology, vol. 61, no. 9, Nov. 2012.

G. Li, H. Yang, L. Cai and L. Gui, “A Lowcomplexity

Equalization Technique for OFDM

System in Time-Variant Multipath Channels,”

in Proc. IEEE on vehicular technology confer-

ence (VTC 2003-Fall), Vol. 4, pp. 2466-2470,

Oct. 2003.

C. Ma, S. Liu and C. Huang, “Low-Complexity

ICI Suppression Methods Utilizing Cyclic Prefix

for OFDM Systems in High-Mobility Fading

Channels,” IEEE Trans. Vehicular Technology,

vol. 63, no. 2, pp. 718-730, Feb. 2014.

P. Reangsuntea, M. Hourai, P. Boonsrimuang,

K. Mori, and H. Kobayashi, “Iterative based ML

Demodulation Method for OFDM Signal under

Higher Mobile Environments,” in Proc. IEEE on

vehicular technology conference (VTC-Spring),

pp. 1-6, May 2015.

P. Reangsuntea, P. Boonsrimuang, K. Mori,

and H. Kobayashi, “Time domain equalization

method for DFTS-OFDM signal without GI under

high mobile environments,” in Proc. of 12nd

International Conference on Electrical Engineer-

ing/Electronics, Computer, Telecommunications

and Information Technology (ECTI-CON), pp.

-6, June 2015.

A. Reangsuntea, P. Reangsuntea, P. Boonsrimuang,

K. Mori, and H. Kobayashi, “Iterative

based Time Domain Equalization Method

for DFTS-OFDM under Highly Mobile Environments,”

in Proc. of 13th International Con-

ference on Electrical Engineering/Electronics,

Computer, Telecommuni- cations and Informa-

tion Technology (ECTI-CON), June 2016.

C. Vulk, “Iterative Solution methods,” Delft

Institute of Applied Mathematics, Netherlands,

Andrew J. Viterbi, “Error Bounds for Convolutional

Codes and an Asymptotically Optimum

Decoding Algorithm,” IEEE Transactions on In-

formation Theory, Volume IT-13, pp. 260-269,

Apr. 1967.