Exact solutions of the fractional Landau-Ginzburg-Higgs equation and the (3+1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation using the simple equation method

Abstract

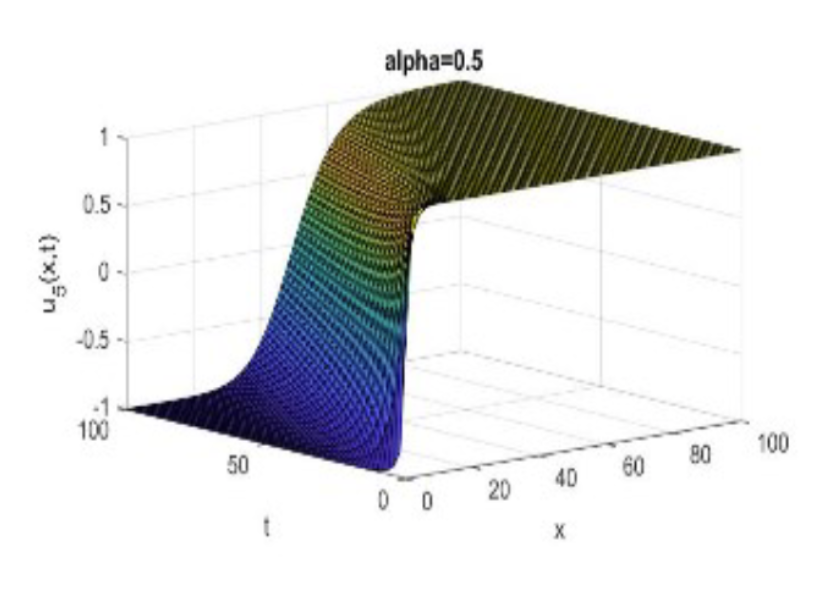
In this article, we analyze the fractional Landau-Ginzburg-Higgs equation and the (3+1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation, two ion wave equations, using the simple equation approach and the Bernoulli equation. The traveling wave solutions are demonstrated by the exponential and hyperbolic functions, which can be interpreted as kink waves. Their graphical representations are three-dimensional graphs, and contour graphs are shown using appropriate parameter values. Additionally, the results demonstrated that the technique employed in this study is a powerful analytical tool for obtaining exact traveling wave solutions to nonlinear models encountered in a variety of scientific and engineering fields.