Comparison of Methods on Asymptotic and Exact Confidence Intervals for a Binomial Proportion with Application

Abstract

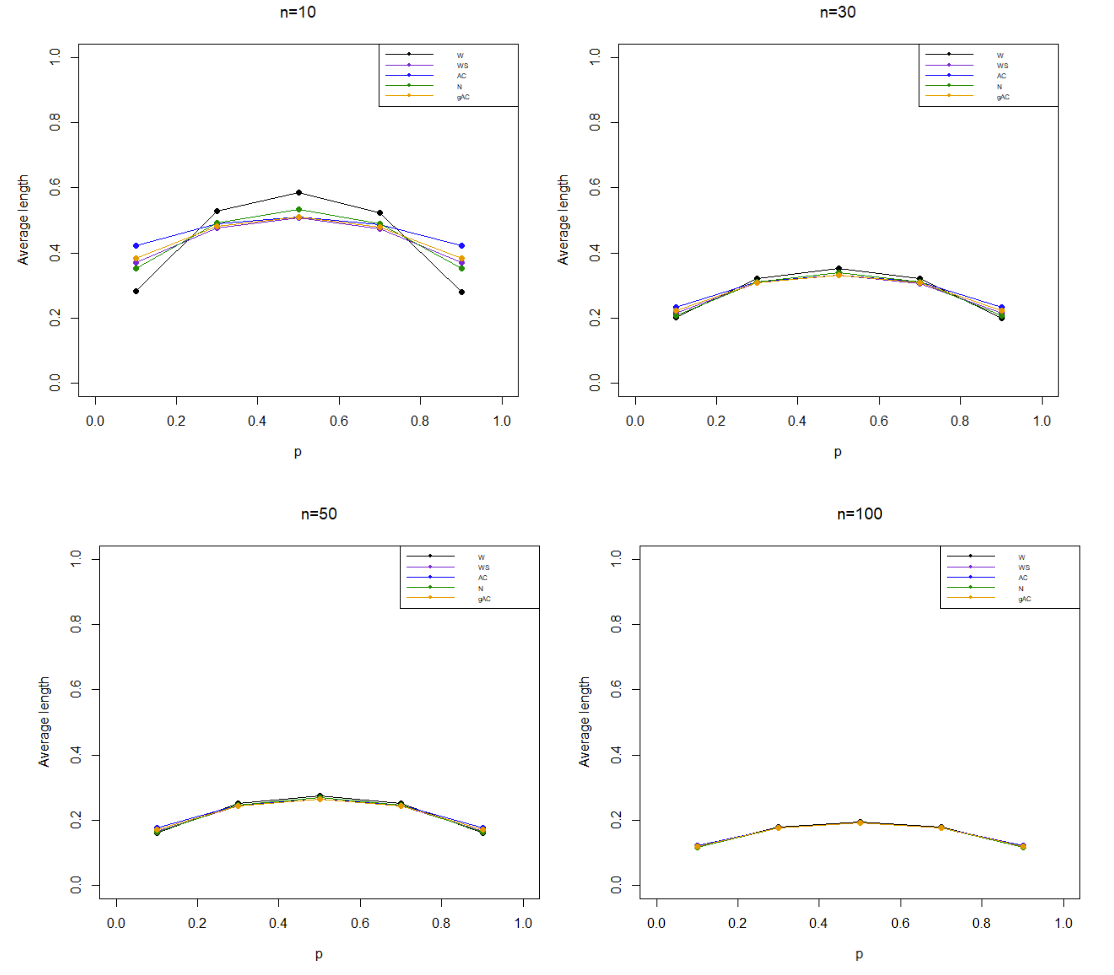
The objective of this research was to compare efficiency of the methods for estimating two types of confidence interval for a binomial proportion, which are exact confidence interval and asymptotic confidence interval by studying comparison upon 5 methods for estimating confidence interval. These 5 methods are Wald method, Wilson Score method, Agresti-Coull method, New method, and generalized Agresti-Coull method.  The data was simulated by using Monte Carlo method, utilizing binomial distribution with parameters   and  that determine sizes of the sample  equal to 10, 30, 50, and 100. Meanwhile, the values of proportion  were determined as 0.1, 0.3, 0.5, 0.7, and 0.9 with confidence level 95% by repeating experiment 10,000 times in each certain circumstance. Moreover, the criteria used to compare efficiency of confidence intervals was coverage probability as well as average length. According to research findings, it can be summarized as follows. Confidence interval of Wilson Score method showed the best efficiency in diverse circumstances in case study. Besides, this confidence interval was appropriate for the circumstance at  when  and  when  was close to 0 or 1, and  for every value of except Furthermore, confidence interval of Agresti-Coull method had the most second efficiency, which was appropriate for  when  and and  when whereas confidence interval of New method had the third most efficiency, which was appropriate for  and  when value of  was close to 0 or 1. At the same time, confidence interval of generalized Agresti-Coull method had the fourth most efficiency, which was appropriate for  when and  However, confidence interval of Wald method possess quite low precision. In addition, confidence interval of these 5 methods can be applicable to the real data in any circumstances.