An Exponential Map-based Whale Optimization Algorithm (Exp-WOA) for Optimization
Main Article Content
Abstract
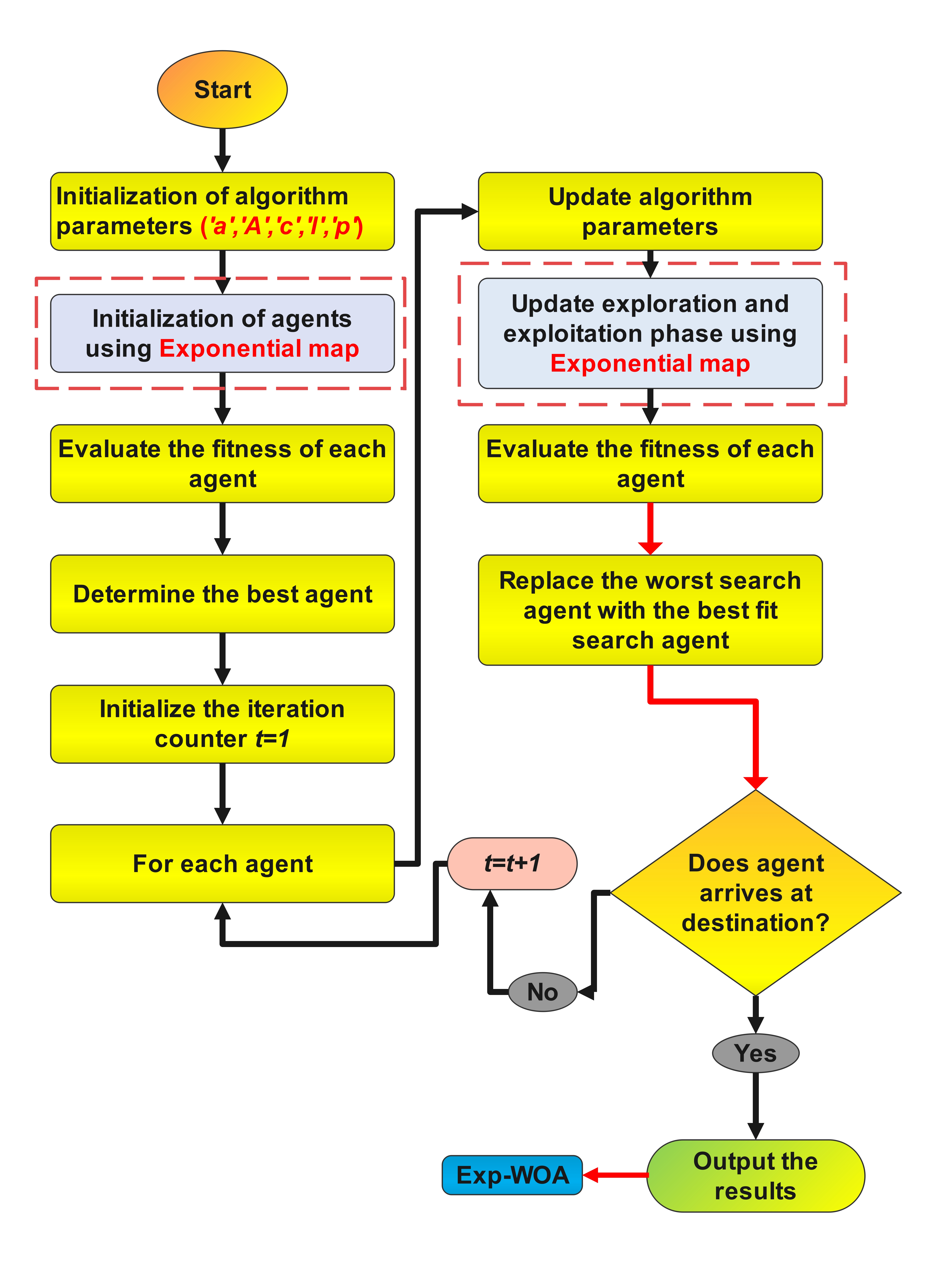
This research work offers three variations of the Whale Optimization Algorithm (WOA) based on exponential chaotic maps, namely Logistic-Exponential-Logistic WOA (LEL-WOA), Logistic-Exponential-Sinusoidal WOA (LES-WOA), and Logistic-Exponential-Tent WOA (LET-WOA). The WOA with an exponential chaos-based mechanism is developed in this study to overcome the poor rate of convergence of the WOA and to prevent getting caught in local optimal solutions while dealing with the challenges. An exponential chaotic mechanism was employed in this research to initialize the agents and control the parameters of the exploration and exploitation phases of WOA. The proposed methodologies (Exp-WOA) are evaluated using twenty-three widely recognized test functions. The results demonstrate that the given solutions can enhance the performance of WOA by achieving optimal (minimum) values. The findings also indicate that LEL-WOA and LES-WOA exhibit faster convergence than WOA.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
G. Kaur and S. Arora, “Chaotic whale optimization algorithm,” Journal of Computational Design and Engineering, vol. 5, no. 3, pp. 275–284, 01 2018. [Online]. Available: https://doi.org/10.1016/j.jcde.2017.12.006
M. O. Okwu and L. K. Tartibu, Metaheuristic Optimization: Nature-Inspired Algorithms Swarm and Computational Intelligence, Theory and Applications. Springer Nature, 2020, vol. 927.
M. J. Heule and O. Kullmann, “The science of brute force,” Communications of the ACM, vol. 60, no. 8, pp. 70–79, 2017.
J. Edmonds, “Matroids and the greedy algorithm,” Mathematical programming, vol. 1, pp. 127–136, 1971.
S. Forrest, “Genetic algorithms,” ACM computing surveys (CSUR), vol. 28, no. 1, pp. 77–80, 1996.
P. Sharma and S. Raju, “Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions,” Soft Computing, pp. 1–64, 2023.
A. Ravindran, G. V. Reklaitis, and K. M. Ragsdell, Engineering optimization: methods and applications. John Wiley & Sons, 2006.
X. Fan, W. Sayers, S. Zhang, Z. Han, L. Ren, and H. Chizari, “Review and classification of bio-inspired algorithms and their applications,” Journal of Bionic Engineering, vol. 17, pp. 611–631, 2020.
S. Y. Ko, I. Gupta, and Y. Jo, “Novel mathematics-inspired algorithms for self-adaptive peer-to-peer computing,” in First International Conference on Self-Adaptive and Self-Organizing Systems (SASO 2007). IEEE, pp. 3–12, 2007.
A. Biswas, K. Mishra, S. Tiwari, and A. Misra, “Physics-inspired optimization algorithms: a survey,” Journal of Optimization, vol. 2013, 2013.
O. D. Montoya, A. Molina-Cabrera, and W. GilGonza ́lez, “A possible classification for metaheuristic optimization algorithms in engineering and science,”Ingenier ́ıa,vol.27,no.3,2022.
E. Rashedi, H. Nezamabadi-Pour, and S. Saryazdi, “Gsa: a gravitational search algorithm,” Information sciences, vol. 179, no. 13, pp. 2232–2248, 2009.
A. Hatamlou, “Black hole: A new heuristic optimization approach for data clustering,” Information sciences, vol. 222, pp. 175–184, 2013.
A. A. Hudaib, H. N. Fakhouri et al., “Supernova optimizer: a novel natural inspired metaheuristic,” Modern Applied Science, vol. 12, no. 1, pp. 32–50, 2018.
A. Kaveh, S. M. Hosseini, and A. Zaerreza, “A physics-based metaheuristic algorithm based on doppler effect phenomenon and mean euclidian distance threshold,” Periodica Polytechnica Civil Engineering, vol. 66, no. 3, pp. 820–842, 2022.
B. Do ̆gan and T. O ̈lmez, “A new metaheuristic for numerical function optimization: Vortex search algorithm,” Information sciences, vol. 293, pp. 125–145, 2015.
L. Abualigah, A. Diabat, S. Mirjalili, M. Abd Elaziz, and A. H. Gandomi, “The arithmetic optimization algorithm,” Computer methods in applied mechanics and engineering, vol. 376, p.113609, 2021.
J.-S. Chou, T. T. P. Pham, and C.-C. Ho, “Metaheuristic optimized multi-level classification learning system for engineering management,” Applied Sciences, vol. 11, no. 12, p. 5533, 2021.
Y. Shi, “Particle swarm optimization,” IEEE connections, vol. 2, no. 1, pp. 8–13, 2004.
M. Dorigo, M. Birattari and T. Stutzle, “Ant colony optimization,” in IEEE Computational Intelligence Magazine, vol. 1, no. 4, pp. 28-39, Nov. 2006.
D. Karaboga, “Artificial bee colony algorithm,” scholarpedia, vol. 5, no. 3, p. 6915, 2010.
S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in engineering software, vol. 95, pp. 51–67, 2016.
D. P. Acharjya and A. P. Kauser, “Swarm intelligence in solving bio-inspired computing problems: Reviews, perspectives, and challenges,” Handbook of Research on Swarm Intelligence in Engineering, pp. 74–98, 2015.
D. P. Heyman and M. J. Sobel, Stochastic models in operations research: stochastic optimization. Courier Corporation, 2004, vol. 2.
K.-L. Du, M. Swamy et al., “Search and optimization by metaheuristics,” Techniques and Algorithms Inspired by Nature, pp.1–10, 2016.
S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in engineering software, vol. 95, pp. 51–67, 2016.
S. Mahmood, N. Z. Bawany, and M. R. Tanweer, “A comprehensive survey of whale optimization algorithm: modifications and classification,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 29, no. 2, p. 899, 2023.
H. M. Mohammed, S. U. Umar, T. A. Rashid et al., “A systematic and meta-analysis survey of whale optimization algorithm,” Computational intelligence and neuroscience, vol. 2019, 2019.
P. P. Jadhav and S. D. Joshi, “Woadf: whale optimization integrated adaptive dragonfly algorithm enabled with the tdd properties for model transformation,” International Journal of Computational Intelligence and Applications, vol. 18, no. 04, p. 1950026, 2019.
M. H. Nadimi-Shahraki, H. Zamani, Z. Asghari Varzaneh, and S. Mirjalili, “A systematic review of the whale optimization algorithm: Theoretical foundation, improvements, and hybridizations,” Archives of Computational Methods in Engineering, pp. 1–47, 2023.
S. Mahdavi, S. Rahnamayan, and K. Deb, “Opposition based learning: A literature review,” Swarm and evolutionary computation, vol. 39, pp. 1–23, 2018.
M. Jiaojiao, L. Guly ́as, and J. Botzheim, “Comparing lamarckian and baldwinian approaches in memetic optimization,” in International Conference on Computational Collective Intelligence. Springer, 2023, pp. 521–533.
Y. Sun, T. Yang, and Z. Liu, “A whale optimization algorithm based on quadratic interpolation for high-dimensional global optimization problems,” Applied Soft Computing, vol. 85, p. 105744, 2019.
P. Du, W. Cheng, N. Liu, H. Zhang, and J. Lu, “A modified whale optimization algorithm with single-dimensional swimming for global optimization problems,” Symmetry, vol. 12, no. 11, p.1892, 2020.
K. Deep and M. Thakur, “A new crossover operator for real coded genetic algorithms,” Applied mathematics and computation, vol. 188, no. 1, pp. 895–911, 2007.
S. Mirjalili, “Sca: a sine cosine algorithm for solving optimization problems,” Knowledge-based systems, vol. 96, pp. 120–133, 2016.
S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Advances in engineering software, vol. 69, pp. 46–61, 2014.
S. M. Almufti, A. A. Shaban, Z. A. Ali, R. I. Ali, and J. A. D. Fuente, “Overview of metaheuristic algorithms,” Polaris Global Journal of Scholarly Research and Trends, vol. 2, no. 2, pp. 10–32, 2023.
H. Ding, Z. Wu, and L. Zhao, “Whale optimization algorithm based on nonlinear convergence factor and chaotic inertial weight,” Concurrency and Computation: Practice and Experience, vol. 32, no. 24, p. e5949, 2020.
H. Li, P. Zou, Z. Huang, C. Zeng and X. Liu, “Multimodal optimization using whale optimization algorithm enhanced with local search and niching technique,” Mathematical Biosciences and Engineering, vol. 17, no. 1, pp. 1–27, 2020.
Y. Guo, H. Shen, L. Chen, Y. Liu and Z. Kang, “Improved whale optimization algorithm based on random hopping update and random control parameter,” Journal of Intelligent & Fuzzy Systems, no. 1, pp. 363-379, 2021.
R. Salgotra, U. Singh and S. Saha, “On some improved versions of whale optimization algorithm,” Arabian Journal for Science and Engineering, vol. 44, no. 11, pp. 9653–9691, 2019.
S. Rahnamayan, H. R. Tizhoosh, and M. M. Salama, “Oppositionbased differential evolution,” IEEE Transactions on Evolutionary computation, vol. 12, no. 1, pp. 64–79, 2008.
M. Cˇrepinˇsek, S.-H. Liu, and M. Mernik, “Exploration and exploitation in evolutionary algorithms: A survey,” ACM computing surveys (CSUR), vol. 45, no. 3, pp. 1–33, 2013.
Q.Fan, Z.Chen, Z.Li, Z.Xia, J.Yu and D. Wang, “A new improved whale optimization algorithm with joint search mechanisms for highdimensional global optimization problems,” Engineering with Computers, pp. 1–28, 2020.
M. P. K. Reddy and M. R. Babu, “Implementing self adaptiveness in whale optimization for cluster head section in internet of things,” Cluster Computing, vol. 22, no. 1, pp. 1361–1372, 2019.
Q. Zhang and L. Liu, “Whale optimization algorithm based on lamarckian learning for global optimization problems,” IEEE Access, vol. 7, pp. 36 642–36 666, 2019.
E. Boesiger, “Evolutionary theories after lamarck and darwin,” in Studies in the Philosophy of Biology. Springer, 1974, pp. 21–44.
R. Deepa and R. Venkataraman, “Enhancing whale optimization algorithm with levy flight for coverage optimization in wireless sensor networks,” Computers & Electrical Engineering, vol. 94, p. 107359, 2021.
S. Dadashzadeh, M. Aghaie and A. Zolfaghari, “Optimal design of separation cascades using the whale optimization algorithm,” Annals of Nuclear Energy, vol. 172, p. 109020, 2022.
B. Alatas, E. Akin and A. B. Ozer, “Chaos embedded particle swarm optimization algorithms,” Chaos, Solitons & Fractals, vol. 40, no. 4, pp. 1715–1734, 2009.
L. dos Santos Coelho and V. C. Mariani, “Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization,” Expert Systems with Applications, vol. 34, no. 3, pp. 1905–1913, 2008.
P. Priyanga, V. V. Pattankar and S. Sridevi, “A hybrid recurrent neural network-logistic chaos-based whale optimization framework for heart disease prediction with electronic health records,” Computational Intelligence, vol. 37, no. 1, pp. 315–343, 2021.
Z. GARI ̇P, M. E. CI ̇MEN, D. KARAYEL, and A. F. BOZ, “The chaos-based whale optimization algorithms global optimization,” Chaos Theory and Applications, vol. 1, no. 1, pp. 51–63, 2019.
Z. Hua and Y. Zhou, “Exponential chaotic model for generating robust chaos,” IEEE transactions on systems, man, and cybernetics: systems, vol. 51, no. 6, pp. 3713–3724, 2019.
L. dos Santos Coelho and V. C. Mariani, “Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization,” Expert Systems with Applications, vol. 34, no. 3, pp. 1905–1913, 2008.
H. Lu, X. Wang, Z. Fei and M. Qiu, “The effects of using chaotic map on improving the performance of multiobjective evolutionary algorithms,” Mathematical Problems in Engineering, vol. 2014, no. 1, p. 924652, 2014.
F. H. Zhou and Z. Z. Liao, “A particle swarm optimization algorithm,” Applied Mechanics and Materials, vol. 303, pp. 1369–1372, 2013.
P. Sharma and S. Raju, “Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions,” Soft Computing, vol. 28, no. 4, pp. 3123–3186, 2024.