A Relational Database Model with Interval Probability Valued Attributes for Uncertain and Imprecise Information
Main Article Content
Abstract
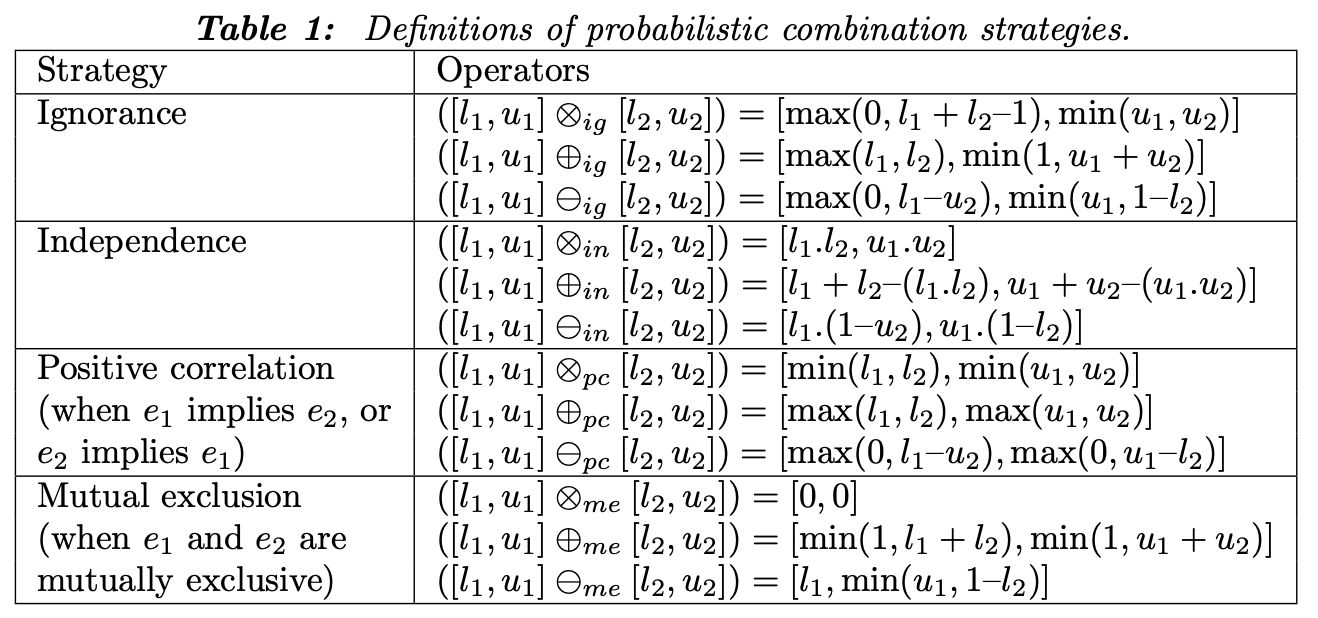
Although the conventional relational database model (CRDB) is benecial to model, design, and implement large-scale systems, it is limited to express and deal with uncertain and imprecise information. In this paper, we introduce a new relational database model as an extension of CRDB where relational attributes may take a value associated with a probability interval, named IPRDB, for representing and handling uncertain and imprecise information in practice. To build IPRDB, we employ three key methods: (1) Probabilistic values of data types are proposed for expressing uncertain and imprecise valued attributes; (2) the probabilistic interpretations of binary relations on sets and operators on probability intervals are used for computing the uncertain degree of functional dependencies, keys, and relations on value domains of attributes; and (3) the combination strategies of probabilistic values are dened for developing new relational algebraic operations. Then, fundamental concepts of the model, such as schemas, probabilistic relations, and probabilistic relational databases, are extended coherently and consistently with those of the conventional relational database model. A set of the properties of the basic probabilistic relational algebraic operations is also formulated and proven. The built IPRDB model can represent and manipulate effectively uncertain and imprecise information in real-world applications.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
E.F. Codd, “A relational model of data for large shared data banks,” Communications of the ACM, vol.13, no.6, pp.377-387, 1970.
G. O ̈zsoyog ̆lu, Z. M. O ̈zsoyo ̆glu, and V. Matos, “Extending relational algebra and relational calculus with set-valued attributes and aggregate functions,” ACM Transactions on Database Systems, vol.12, no.4, pp.566-592, 1987.
A. Silberschatz, H.F. Korth, and S. Sudarshan, Database system concepts, Seventh Edition, McGraw-Hill, 2019.
D. Dey and S. Sarkar, “A probabilistic relational model and algebra,” ACM Transactions on Database Systems, vol.21, no.3, pp.339-369, 1996.
D. Barbara, H. Garcia-Molina, and D. Porter, “The management of probabilistic data,” IEEE Transactions on Knowledge and Data Engineering, vol.4, no.5, pp.487-502, 1992.
J. Bernad, C. Bobed, and E. Mena, “Uncertain probabilistic range queries on multidimensional data,” Information Sciences, vol. 537, pp.334-367, 2020.
A. Ali, S. Talpur, and S. Narejo, “Detecting faulty sensors by analyzing the uncertain data using probabilistic databases,” Proceedings of 3rd International Conference on Computing, Mathematics and Engineering Technologies, Sukkur, Pakistan, pp.143-150, 2020.
V.V. Kheradkar and S. K. Shirgave, “Query processing over relational cross model in uncertain and probabilistic databases,” Proceedings of 3Th International Conference on Artificial Intelligence and Smart Energy, Coimbatore, India, pp.763-769, 2023.
N. Fuhr and T. Rolleke, “A probabilistic relational algebra for the integration of information retrieval and database systems,” ACM Transactions on Information Systems, vol.15, no.1, pp.32-66, 1997.
S. Zhang and C. Zhang, “A probabilistic data model and its semantics,” Journal of Research and Practice in Information Technology, vol.35, no.4, pp.237-256, 2003.
Z. Ma and L. Yan, Advances in probabilistic databases for uncertain information management, Springer-Verlag Berlin Heidelberg, 2013.
Y. Li, J. Chen, and L. Feng, “Dealing with uncertainty: A survey of theories and practices,” IEEE Transactions on Knowledge and Data Engineering, vol. 25, no.11, pp.2463-2482, 2013.
I.I. Ceylan, A. Darwiche, and G.V.D. Broeck, “Open-world probabilistic databases: Semantics, algorithms, complexity,” Journal of Artificial Intelligence, vol.295, no.11, pp.103474-103513, 2021.
H. Debbi, “Explaining query answers in probabilistic databases,” International Journal of Interactive Multimedia and Artificial Intelligence, vol.8, no.4, pp.140-152, 2023.
L.V.S. Lakshmanan, N. Leone, R. Ross, and V.S. Subrahmanian, “Probview: A flexible probabilistic database system,” ACM Transactions on Database Systems, vol.22, no.3, pp.419-469, 1997.
W. Zhao, A. Dekhtyar, and J. Goldsmith, “Databases for interval probabilities,” International Journal of Intelligent Systems, vol.19, no.9, pp.789-815, 2004.
R. Ross and V.S. Subrahmanian, “Aggregate operators in probabilistic databases,” Journal of the ACM, vol.52, no.1, pp.54-101, 2005.
D. Dey and S. Sarkar, “Generalized normal forms for probabilistic relational data,” IEEE Transactions on Knowledge and Data Engineering, vol.14, no.3, pp.485-497, 1992.
T. Eiter, T. Lukasiewicz, and M. Walter, “A data model and algebra for probabilistic complex values,” Annals of Mathematics and Artificial Intelligence, vol.33, pp.205-252, 2001.
S.K. Lee, “An extended relational database model for uncertain and imprecise information,” Proceedings of 18th Conference on Very Large Data Bases, Vancouver, Canada, pp.211-220, 1992.
H. Nguyen, “A probabilistic relational database model and algebra,” Journal of Computer Science and Cybernetics, vol.31, no.4, pp.305-321, 2015.
H. Nguyen, T.N. Nguyen, and T.T.N. Tran, “A probabilistic relational database model with uncertain multivalued attributes,” ICIC Express Letters, vol. 16, no.3, pp.241-248, 2022.
H. Nguyen, “Extending probabilistic relational database model with uncertain multivalued attributes,” International Journal of Innovative Computing, Information and Control, vol.18, no.5, pp.1477–1492, 2022.
V. Biazzo, R. Giugno, T. Lukasiewicz, and V. S. Subrahmanian, “Temporal probabilistic object bases,” IEEE Transactions on Knowledge and Data Engineering, vol.15, no.4, pp. 921-939, 2003.
H. Nguyen, “Extending relational database model for uncertain information,” Journal of Computer Science and Cybernetics, vol.35, no.4, pp.355-372, 2019.
T. Friedman and G. Broeck, “Symbolic querying of vector spaces: probabilistic databases meet relational embeddings,” Proceedings of 36th Conference on Uncertainty in Artificial Intelligence, Toronto, Canada, vol.124, pp.1268-1277, 2020.
A. Gilad, A. Imber, and B. Kimelfeld, “The consistency of probabilistic databases with independent cells,” Proceedings of 26th International Conference on Database Theory, Ioannina, Greece, pp. 22:1-22:19, 2023.
T.V. Bremen and K.S. Meel, “Probabilistic query evaluation: The combined FPRAS landscape,” Proceedings of 42th ACM SIGMODSIGACT-SIGAI Symposium on Principles of Database Systems, New York, USA, pp 339–347, 2023.