Compact Genetic Algorithm with Quantum-Assisted Feasibility Enforcement
Main Article Content
Abstract
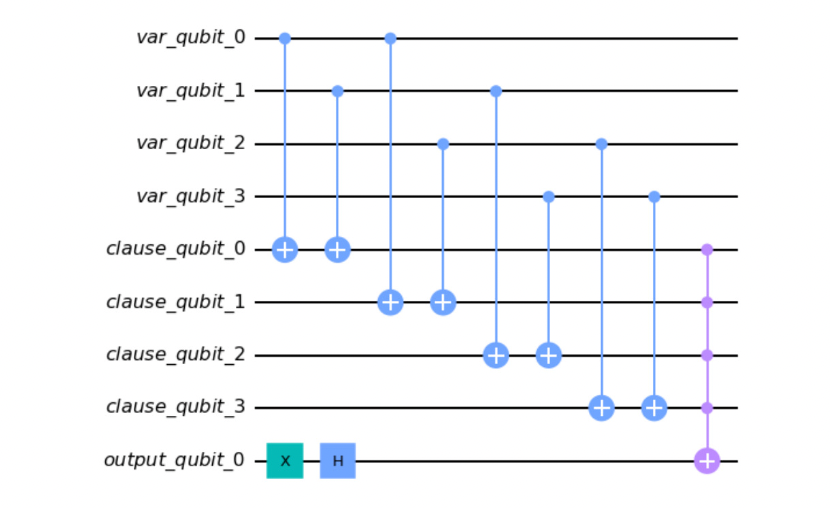
The local optima problem is one of the biggest obstacles in compact genetic algorithms since each bit in the problem encoding string is independent of the others. We propose a quantum-assisted compact genetic algorithm that uses a quantum amplitude amplification technique in the selection process to circumvent the said problem. In addition to using elitism mechanics where a single best candidate solution is kept to drive the probability vector, the amplitude amplification subroutine also acts as a mutation operator which, with high probability, enforces the constraint that the newly generated candidate is a feasible solution. We demonstrate this idea by applying the algorithm to the traveling salesman problem of size 3 and 4 cities on IBM Qiskit simulator to show how one would construct the quantum circuit and how to encode the optimization problem into quantum states via Ising spin model encoding. We then show space and time complexity analysis based on the quantum circuit model. Finally, we discuss the number of qubits required for encoding, gate counts in the circuit model, and the practicality of applying this to a small-scale devices in the future.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
D. E. Goldberg, D. E. Goldberg, G. Goldberg, David Edward, and V. A. P. o. H. D. E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley.
O. Roeva, S. Fidanova, and M. Paprzycki, “Influence of the Population Size on the Genetic Algorithm Performance in Case of Cultivation Process Modelling,” p. 6.
A. Rodionova, K. Antonov, A. Buzdalova, and C. Doerr, “Offspring Population Size Matters when Comparing Evolutionary Algorithms with Self-Adjusting Mutation Rates,” in Proceedings of the Genetic and Evolutionary Computation Conference, pp. 855–863. [Online]. Available: http://arxiv.org/abs/1904.08032
D. Mora-Melia`, F. J. Mart ́ınez-Solano, P. L. Iglesias-Rey, and J. H. Gutierrez-Bahamondes, “Population Size Influence on the Efficiency of Evolutionary Algorithms to Design Water Networks,” vol. 186, pp. 341–348. [Online]. Available: https://www.sciencedirect.com/ science/article/pii/S1877705817313565
G. Harik, E. Cantu-Paz, D. E. Goldberg, and B. L. Miller, “The gambler’s ruin problem, genetic algorithms, and the sizing of populations,” vol. 7, no. 3, pp. 231–253.
C. W. Ahn, K. P. Kim, and R. S. Ramakrishna, “A memory-efficient elitist genetic algorithm,” in International Conference on Parallel Processing and Applied Mathematics, Springer, 2003, pp. 552–559.
U. F. Siddiqi, Y. Shiraishi, and S. M. Sait, “Memory-efficient genetic algorithm for path optimization in embedded systems,’ IPSJ Online Transactions, vol. 6, pp. 28–36, 2013.
C. T. Joseph, K. Chandrasekaran, and R. Cyr- iac, “Improving the efficiency of genetic algorithm approach to virtual machine allocation,” in 2014 International Conference on Computer and Communication Technology (ICCCT). IEEE, 2014, pp. 111–116.
D. R. da S. Medeiros, M. F. Torquato, and M. A. Fernandes, “Embedded genetic algorithm for low-power, low-cost, and low-size-memory devices,” Engineering Reports, vol. 2, no. 9, p. e12231, 2020.
G. Harik, F. Lobo, and D. Goldberg, “The compact genetic algorithm,” vol. 3, no. 4, pp. 287–297.
P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” SIAM Journal on Com- puting, vol. 26, no. 5, p. 1484–1509, Oct 1997. [Online]. Available:http://dx.doi.org/ 10.1137/S0097539795293172
R. P. Feynman, “Simulating physics with com- puters,” vol. 21, no. 6, pp. 467–488. [Online]. Available: https://doi.org/10.1007/BF02650179
X. Ma, X. Yuan, Z. Cao, B. Qi, and Z. Zhang, “Quantum random number generation,” vol. 2, no. 1, pp. 1–9. [Online]. Available: https:// www.nature.com/articles/npjqi201621
Z. Brakerski, P. Christiano, U. Mahadev, U. Vazirani, and T. Vidick, “A Cryptographic Test of Quantumness and Certifiable Randomness from a Single Quantum Device,” [Online]. Available: urlhttp://arxiv.org/abs/1804.00640
L. K. Grover, “A fast quantum mechanical algorithm for database search,” in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, ser. STOC ’96. Association for Computing Machinery, pp. 212–219. [Online]. Available: https://doi. org/10.1145/237814.237866
W. P. Baritompa, D. W. Bulger, and G. R. Wood, “Grover’s quantum algorithm applied to global optimization,” SIAM Journal on Optimization, vol. 15, no. 4, pp. 1170–1184, 2005.
M. Furer, “Solving np-complete problems with quantum search,” in Latin American Symposium on Theoretical Informatics, Springer, 2008, pp. 784–792.
G. Sun, S. Su, and M. Xu, “Quantum algorithm for polynomial root finding problem,” in 2014 Tenth International Conference on Computational Intelligence and Security, IEEE, 2014, pp. 469–473.
A. Kirke, “Application of grover’s algorithm on the ibmqx4 quantum computer to rule-based algorithmic music composition,” CoRR, 2019.
R. Preston, “Applying grover’s algorithm to hash functions: A software perspective,” arXiv preprint arXiv:2202.10982, 2022.
A. Narayanan and M. Moore, “Quantuminspired genetic algorithms,” in Proceedings of IEEE International Conference on Evolutionary Computation, 1996, pp. 61–66.
Z. A. E. M. Dahi, C. Mezioud, and A. Draa, “A quantum-inspired genetic algorithm for solving the antenna positioning problem,” Swarm and Evolutionary Computation, vol. 31, pp. 24–63, 2016.
W. Chmiel and J. Kwiecien ́, “Quantum-inspired evolutionary approach for the quadratic assignment problem,” Entropy, vol. 20, no. 10, 2018. [Online]. Available: https://www.mdpi.com/ 1099-4300/20/10/781
J. King et al., “Quantum-assisted genetic algorithm,” 2019.
J. Supasil, P. Pathumsoot, and S. Suwanna, “Simulation of implementable quantum-assisted genetic algorithm,” Journal of Physics: Conference Series, vol. 1719, no. 1, p. 012102, jan 2021. [Online].Available: https://doi.org/10.1088/1742-6596/1719/1/012102
A. Malossini, E. Blanzieri, and T. Calarco, “Quantum genetic optimization,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 2, pp. 231–241, 2008.
H. Wang, J. Liu, J. Zhi, and C. Fu, “The improvement of quantum genetic algorithm and its application on function optimization,” Mathematical Problems in Engineering, vol. 2013, 05 2013.
S. Yingchareonthawornchai, C. Aporntewan, and P. Chongstitvatana, “An implementation of compact genetic algorithm on a quantum computer,” in 2012 Ninth International Conference on Computer Science and Software Engineering (JCSSE), 2012, pp. 131–135.
B. Rylander, T. Soule, J. Foster, and J. AlvesFoss, “Quantum genetic algorithms,” 01 2000, p. 373.
A. Layeb and D. Saidouni, “Quantum genetic algorithm for binary decision diagram ordering problem,” 2007.
Z. Laboudi and S. Chikhi, “Evolving cellular automata by parallel quantum genetic algorithm,” in 2009 First International Conference on Net- worked Digital Technologies, 2009, pp. 309–314.
A. Lucas, “Ising formulations of many NP problems,” Frontiers in Physics, vol. 2, 2014. [Online]. Available: http://dx.doi.org/10. 3389/fphy.2014.00005
M. S. ANIS et al., “Qiskit: An open-source framework for quantum computing,” 2021.
E. Farhi, J. Goldstone, and S. Gutmann, “A Quantum Approximate Optimization Algorithm,” [Online]. Available: http://arxiv. org/abs/1411.4028
A. N. Sloss and S. Gustafson, “2019 Evolutionary Algorithms Review,” in Genetic Programming Theory and Practice XVII, ser. Genetic and Evolutionary Computation, W. Banzhaf, E. Goodman, L. Sheneman, L. Trujillo, and B. Worzel, Eds. Springer International Publishing, pp. 307–344. [Online]. Available: https://doi.org/10.1007/978-3-030-39958-016
T. B ̈ack, Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms, USA:Oxford University Press, Inc., 1996.
C. Aporntewan and P. Chongstitvatana, “A hardware implementation of the compact genetic algorithm,” in Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No.01TH8546), vol. 1, 2001, pp. 624–629 vol. 1.
G. Huang and L. Wang, “Hybrid Neural Network Models for Hydrologic Time Series Forecasting Based on Genetic Algorithm,” in 2011
Fourth International Joint Conference on Computational Sciences and Optimization, 2011, pp. 1347–1350.
M. Musnjak and M. Golub, “Using a set of elite individuals in a genetic algorithm,” in 26th International Conference on Information Technology Interfaces 2004, vol. 1, pp. 531–535, 2004.
L. Gaxiola, J. Tapia, and V. Diaz-Ramirez, “Parallel Genetic Algorithms on a GPU to Solve the Travelling Salesman Problem,” 2014.
M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed. Cambridge University Press.
G. Brassard, P. Hoyer, M. Mosca, and A. Tapp, “Quantum Amplitude Amplification and Estimation,” [Online]. Available: http://arxiv. org/abs/quant-ph/0005055
M. Boyer, G. Brassard, P. Hoeyer, and A. Tapp, “Tight bounds on quantum searching,” vol. 46, no. 4-5, pp. 493–505. [Online]. Available: http: //arxiv.org/abs/quant-ph/9605034
S. Aaronson and A. Ambainis, “The Need for Structure in Quantum Speedups,” [Online]. Available: http://arxiv.org/abs/0911.0996
A. B ̈artschi and S. Eidenbenz, “Grover Mixers for QAOA: Shifting Complexity from Mixer Design to State Preparation,” in 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), pp. 72–82.
Y. Nam, N. J. Ross, Y. Su, A. M. Childs, and D. Maslov, “Automated optimization of large quantum circuits with continuous parameters,” npj Quantum Information, vol. 4, no. 1, p. 23, May 2018. [Online]. Available: https://doi. org/10.1038/s41534-018-0072-4
E.Mun ̃oz-CoreasandH.Thapliyal,“T-count and Qubit Optimized Quantum Circuit Design of the Non-Restoring Square Root Algorithm,” dec 2017. [Online]. Available: http://arxiv. org/abs/1712.08254
C. S. Cheng, A. K. Singh, and L. Gopal, “Efficient Three Variables Reversible Logic Synthesis Using Mixed-polarity Toffoli Gate,” Procedia Computer Science, vol. 70, pp. 362–368, 2015. [Online]. Available: https://www.sciencedirect.com/science/ article/pii/S1877050915031993
T. Morimae, K. Fujii, and H. Nishimura, “Power of one non-clean qubit,” oct 2016. [Online]. Available: https://arxiv.org/abs/ 1610.07244
J. Preskill, “Quantum Computing in the NISQ era and beyond,” jan 2018. [Online]. Available: http://arxiv.org/abs/1801.00862http:// dx.doi.org/10.22331/q-2018-08-06-79
M. McEwen, L. Faoro, K. Arya, A. Dunsworth, T. Huang, S. Kim, B. Burkett, A. Fowler, F.
C. Durr and P. Hoyer, “A Quantum Algorithm for Finding the Minimum,” [Online]. Available: http://arxiv.org/abs/quant-ph/9607014
S. Forrest and M. Mitchell, “Relative Building-Block Fitness and the Building- Block Hypothesis,” in Foundations of Genetic Algorithms, ser. Foundations of Genetic Algorithms, L. D. Whitley, Ed. Elsevier, vol. 2, pp. 109–126. [Online]. Available: https://www.sciencedirect.com/science/ article/pii/B9780080948324500131