Enhancement of Gravitational Search Algorithm using A Differential Mutation Operator and Its Application on Reconstructing Gene Regulatory Network
Main Article Content
Abstract
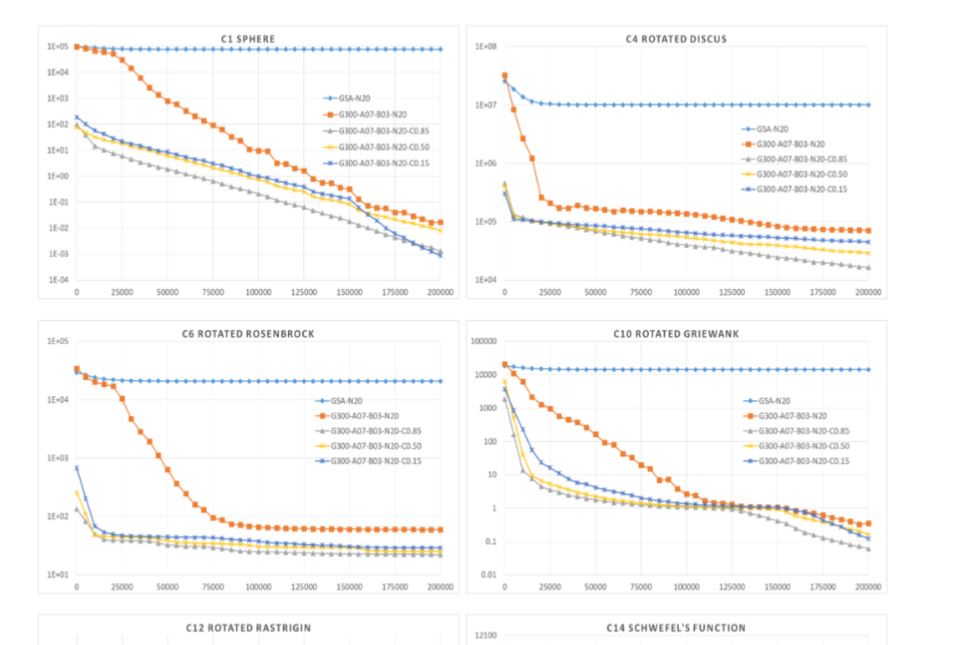
Gravitational Search Algorithm (GSA) is a recent stochastic search algorithm that is inspired from the concepts of gravity rule and law of motion in physics. Despite its success and attractiveness, it has some coefficients and parameters that should be properly tuned to improve its performance. This paper studies the performance of GSA by varying the parameters that controls its gravitational force. Then a new differential mutation operator is proposed to enhance performance of GSA by accelerating its convergence. The proposed algorithm, namely DMGSA, is evaluated using 15 well-known benchmark functions from the special session of CEC2013 with different characteristics including randomly shifted optimum, rotation and non-separability. The results obviously confirms the performance achieved from the proposed mutation operator outperforms that from the attempts of parameter tuning in the original GSA. Lastly, DMGSA is applied for optimizing a small-scale gene regulatory network. The result demonstrates that its performance is highly competitive and clearly surpasses original GSA.
Article Details
References
E. Rashedi, H. Nezamabadi-Pour, S. Saryazdi, “GSA: a gravitational search algorithm,” Inf Sci, vol.179, no.13, pp.2232–48, 2009.
B. Shaw, V. Mukherjee, S.P. Ghoshal, "A novel opposition-based gravitational search algorithm for combined economic and emission dispatch problems of power systems," International Journal of Electrical Power & Energy Systems, vol.35, no.1, pp.21-33, 2012.
M. Khatibinia, S. Khosravi, “A hybrid approach based on an improved gravitational search algorithm and orthogonal crossover for optimal shape design of concrete gravity dams,” Appl. Soft Comput. J., vol.16, pp.223–233, 2014.
T. Ganesan, et al., “Swarm intelligence and gravitational search algorithm for multi-objective optimization of synthesis gas production,” Appl. Energy, vol.103, pp.368–374, 2013.
D.L.G. Alvarez, et al., “Comparing multiobjective swarm intelligence metaheuristics for DNA motif discovery,” Eng. Appl. Artif. Intell., vol.26, no.1, pp.314–326, 2013.
T. Chakraborti, K. Das Sharma, A. Chatterjee, “A novel local extrema based gravitational search algorithm and its application in face recognition using one training image per class,” Eng. Appl. Artif. Intell. vol.34, pp.13–22, 2014.
M. Yin, et al., “A novel hybrid K-harmonic means and gravitational search algorithm approach for clustering,” Expert Syst. Appl., vol.38, no. 8, pp.9319–9324, 2011.
X. Han, et al., “Feature subset selection by gravitational search algorithm optimization,” Inf. Sci. vol. 281, pp.128–146, 2014.
R.-C. David, et al., “Gravitational search algorithm-based design of fuzzy control systems with a reduced parametric sensitivity,” Inf. Sci., vol. 247, pp. 154–173, 2013.
E. Rashedi, E. Rashedi, H. Nezamabadi-pour, “A comprehensive survey on gravitational search algorithm,” Swarm and Evolutionary Computation, pp.1-18, 2017.
G. Sun, A. Zhang, Z. Wang, Y. Yao, J. Ma, G.D. Couples, “Locally informed gravitational search algorithm,” Knowl Based Syst, vol.104, pp.134–44, 2016.
R. Storn, K. Price, “Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, pp. 341–359, 1997.
S. Das, P. N. Suganthan, "Differential Evolution: A Survey of the State-of-the-Art," in IEEE Transactions on Evolutionary Computation, vol.15, no.1, pp. 4-31, Feb. 2011.
S. Sarafrazi, H. Nezamabadi-pour, S. Saryazdi, "Disruption: A new operator in gravitational search algorithm," Scientia Iranica, Volume 18, Issue 3, pp.539-548, 2011.
M. Doraghinejad, H. Nezamabadi-pour, “Black hole: a new operator for gravitational search algorithm,” Int. J. Comput. Intell. Syst. vol.7, no.5, pp.809–826, 2014.
X. Li, M. Yin and Z. Ma, “Hybrid differential evolution and gravitation search algorithm for unconstrained optimization,” Int’ J. of the Physical Sciences, vol.6, no.25, pp.5961-5981.
Baoyong Yin, Zhaolu Guo, Zhengping Liang, Xuezhi Yue, "Improved gravitational search algorithm with crossover," Computers & Electrical Engineering, vol. 66, pp.505-516, 2018.
J.J. Liang, B.Y. Qu, P.N. Suganthan, and A.G. Herńandez-Daz, “Problem definitions and evaluation criteria for the CEC 2013 special session on real-parameter optimization,” Nanyang Technological University, Tech. Rep., 2013.
J. Kennedy, R.C. Eberhart, “Particle swarm optimization,” Proc. of IEEE Int’ Conf. on Neural Networks. Piscataway, NJ, 1995, pp. 1942-1948.
W.-P. Lee, Y.-T. Hsiao, “Inferring gene regulatory networks using a hybrid GA-PSO approach with numerical constraints and network decomposition,” Information Sciences, vol.188, pp.80-99, 2012.
M.A. Savageau, Biochemical Systems Analysis. A Study of Function and Design in Molecular Biology. Addison-Wesley, 1976.
D. Tominaga, N. Koga, and M. Okamoto, “Efficient Numerical Optimization Algorithm Based on Genetic Algorithm for Inverse Problem,” Proc. Genetic and Evolutionary Computation Conf., pp. 251-258, July 2000.
N. Noman, H. Iba. Inference of gene regulatory networks using s-system and differential evolution. In Genetic and Evolutionary Computation Conference, Washington, DC, pp.439–446, 2005.
C. Worasucheep, "An opposition-based hybrid artificial bee colony with differential evolution," 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, pp. 2611-2618, 2015.
K.-Y. Tsai, F.-S. Wang, “Evolutionary Optimization with Data Collocation for Reverse Engineering of Biological Networks,” Bioinformatics, vol. 21, no. 7, pp.1180-1188, 2005.