The Completed Probabilistic Modelling of Nanometer MIFGMOSFET
Main Article Content
Abstract
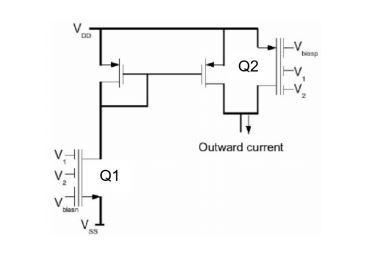
A completed model of the probabilistic distribution of the drain current’s random variation of the nanometer multiple input floating gate MOSFET (MIFGMOSFET) is proposed in this work. The modelling process has taken the dominant physical level causes of the drain current’s variations into account. Unlike its predecessor, the proposed model considers both N-type and P-type nanometer MIFGMOSFET. Moreover, the formerly neglected parasitic coupling capacitances have also been taken into account. The obtained modelling results, which are based on the derived drain current’s equations of nanometer MIFGMOSFET, are very accurate. They can predict the probabilistic distributions of the candidate N-type and P-type nanometer MIFGMOSFETs obtained by using Monte-Carlo simulations with 99% confidence and higher accuracy than that of the previous work. We also perform a comparative robustness study of the nanometer MIFGMOSFET of both types and demonstrate various interesting applications of our modelling results
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
S.K. Saha, “Design Considerations for Sub-90 nm Split-Gate Flash Memory Cells,” IEEE Transactions on Electron Devices, Vol. 54, No. 11, pp. 3049–3055, 2007.
S.K. Saha, “Scaling Considerations for Sub-90 nm Split-Gate Flash Memory Cells,” IET circuits, devices & systems, Vol. 2, No. 1, pp. 144-150, 2008. 208 ECTI TRANSACTIONS ON COMPUTER AND INFORMATION TECHNOLOGY VOL.14, NO.2 November 2020
S.K. Saha, “Non-linear Coupling Voltage of Split Gate Memory Cells with Additional Top Coupling Gate,” IET circuits, devices & systems, Vol.6, No. 3, pp. 204-210, 2012
C-W. Cao, S-G. Zang, X. Lin, Q-Q. Sun, C. Xing, P-F. Wang, and D. W. Zhang, “A Novel 1T-1D DRAM Cell for Embedded Application,” IEEE Transactions on Electron Devices, Vol. 59, No. 5, pp. 1304-1310, 2012.
D. Schinke, N. D. Spigna, M. Shiveshwarkar, and P. Franzon, “Computing with Novel Floating Gate Devices,” Computer, Vol. 44, No. 2, pp. 29-36, 2011.
R. Pandey and M. Gupta, “FGMOS based Voltage Controlled Grounded Resistor,” Radio Engineering, Vol. 19, No. 3, pp. 455–459, 2010
V. Suresh Babu, R.S. Devi, A. Sekhar amd M.R. Baiju, “FGMOSFET Circuit for Neuron Activation Function and Its Derivative,” Proceedings of the 4th IEEE conference on industrial electronics and applications (ICIEA09), pp. 739–744, 2009.
E. Rodriguez-Villegas, A. Yufera and A. Rueda, “A 1.25-V Micropower Gm-C Filter Based on FGMOS Transistors Operating in Weak Inversion,” IEEE Journal of Solid-State Circuits, Vol. 39, No. 1, pp. 100–111, 2004
B. Ramasubramanian, “A New Wide Input-range FGMOS Based Four Quadrant Multiplier with Electrical Error Correction,” Proceedings of the 2007 International Symposium on Signals, Circuits and Systems (ISCAS07), pp. 1-4, 2007
S. Vlassis and S. Siskos, “Design of Voltage-mode and Current-mode Computational Circuits using Floating-Gate MOS Transistors,” IEEE Transactions on Circuits and Systems I: Regular Papers, Vol. 51, No. 2, pp. 329-341, 2004.
Y. Zhai and P. A. Abshire, “Adaptive Log Domain Filters for System Identification using Floating Gate Transistors,” Analog Integrated Circuits and Signal Processing, Vol.56, No. 1-2, pp.23–36, 2008.
K. Hasegawa, M. Aoki, T. Yamawaki, S. Tanaka, “Modeling Transistor Variation Using α-power Formula and Its Application to Sensitivity Analysis on Harmonic Distortion in Differential Amplifier,” Analog Integrated Circuits and Signal Processing, Vol. 72, No. 3, pp 605–613, 2012.
R. Banchuin and R. Chaisricharoen. “The Probabilistic Modeling of Random Variation in FGMOSFET,” Proceedings of the 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), pp. 1-4, 2016.
R. Banchuin and R. Chaisricharoen, “Probabilistic Modelling of Variation in FGMOSFET,” ECTI Transactions on Computer and Information Technology, Vol. 11, No. 1, 50-62, 2017.
R. Banchuin and R. Chaisricharoen, “Probabilistic Model of Nanometer MIFGMOSFET,” Proceedings of the 14th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), pp. 781-784, 2017.
L. Bisdounis, “Short Circuit Energy Dissipation Model for Sub 100 nm CMOS Buffers,” Proceedings of the 17th IEEE International Conference on Electronics, Circuits, and Systems (ICECS), pp. 615-618, 2010.
K. Takeuchi, A. Nishida and T. Hiramoto, “Random Fluctuations in Scaled MOS Devices,” Proceedings of the 2009 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD09), pp. 79-85, 2009.
J. Ramirez-Angulo, G. Gonzlrlez-Altamirano and S. C. Choi, “Modeling Multiple-input Floating-gate Transistors for Analog Signal Processing,” Proceedings of the 1997 International Symposium on Signals, Circuits and Systems (ISCAS97), pp. 2020-2023, 1997.
A.H. Haddad, Probabilistic Systems and Random Signals, Prentice Hall, New Jersey, 2006.
G. Cijan, T. Tuma and A. Burmen, “Modelling and Simulation of MOS Transistor Mismatch,” Proceeding of the 6th Eurosim Congress on Modeling and Simulation (EUROSIM 07), pp. 1-8, 2007.
G. Daryanani, Principle of Active Network Synthesis and Design, John Wiley and sons, Inc., New York, 1976.
S.A. Klugman, H.H Panjer and G.E. Willmot, Loss Models: From Data to Decisions, John Wiley and Sons, Inc., New York, 2008.
W.W. Hines, D.C. Montgomery, D.M. Goldsman and C.M. Borror, Probability and Statistics in Engineering, John Wiley and Sons, Inc., New York, 2003.
C. Forbes, M. Evans, N. Hastings and B. Peacock, Statistical Distributions, 4th ed., John Wiley and Sons, Inc., New York, 2011.