STABILITY ANALYSIS AND OPTIMAL CONTROL FOR HIV INFECTION WITHIN-HOST MODEL WITH IMMUNE RESPONSE AND ANTIRETROVIRAL TREATMENT

Ratchada Viriyapong; Bunsarika Laokhetkid

Authors

Ratchada Viriyapong Department of Mathematics, Faculty of Science, Naresuan University, Thailand
Bunsarika Laokhetkid Department of Mathematics, Faculty of Science, Naresuan University, Thailand

Keywords:

HIV infection, immune response, immune impairment, antiretroviral treatment, optimal control

Abstract

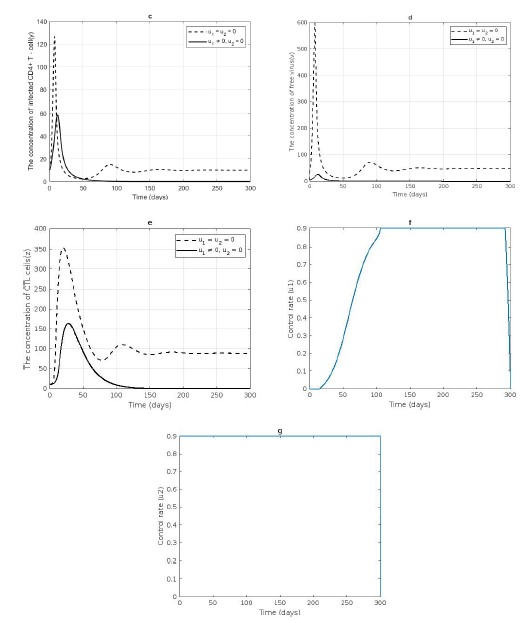
In this study, we propose a within-host treatment model for HIV infection of CD4+ T-cells. The model includes immune response, immune impairment, and antiretroviral treatment. Two types of antiretroviral drugs (reverse transcriptase inhibitors (RTIs) and protease inhibitors (PIs)) are used within the model. Positivity and boundedness of solutions are verified. We present two equilibrium points which are infection-free and infected one. The basic reproduction number is calculated, and it becomes the threshold indicating the stability of each equilibrium point. When it is less than a unity, an infection-free equilibrium point is locally stable, whereas when it is greater than one an infected equilibrium point exists, and it is locally stable with some required conditions. Global stability of infection-free equilibrium point is obtained with some conditions. Further, we extend the model by applying optimal control problem in which both antiretroviral drugs becomes control variables. This is to minimize the HIV infection of CD4+ T-cells. Our numerical results demonstrate that RTIs drug alone could slightly reduce an HIV infection whereas the PIs drug alone gives better result in reducing the infection than RTIs drug. However, a combination of both types of drugs gives the best result for eliminating an HIV infection of CD4+ T-cells.

References

Arenas, A. J., González-Parra, G., Naranjo, J. J., Cogollo, M., & De La Espriella, N. (2021). Mathematical analysis and numerical solution of a model of HIV with a discrete time delay. Mathematics, 9(3), 257. http:// doi.org/10.3390/math9030257.

Arruda, E. F., Dias, C. M., de Magalhã, C. V., Pastore, D. H., Thomé , R. C., & Yang, H. M. (2015). An optimal control approach to HIV immunology. Applied Mathematics, 6(6), 1115-1130. https://doi.org/10.4236/am.2015.66102.

Arts, E. J., & Hazuda, D. J. (2012). HIV-1 antiretroviral drug therapy. Cold Spring Harbor perspectives in medicine,2(4): a007161. https://doi.org/10.1101/cs-hperspect.a007161.

Ayele, T. K., Goufo, E. F. D., & Mugisha, S. (2021). Mathematical modeling of HIV/AIDS with optimal control: a case study in Ethiopia. Results in Physics, 26, 104263. https://doi.org/10.1016/j.rinp.2 021.1042 63.

Bai, N., & Xu, R. (2021). Mathematical analysis of an HIV model with latent reservoir, delayed CTL immune response and immune impairment. Mathematical Biosciences and Engineering, 18(2), 1689-1707.https://doi.org/10.3934/mbe.2021087.

Jones, A. (2021). Types of antiretroviral medications. RetrievedFebruary9, 2023, from https://www.aidsmap.com/about-hiv/types-antiretroviral medications

Karrakchou, J., Rachik, M., & Gourari, S. (2006). Optimal control and infectiology: application to an HIV/AIDS model. Applied mathematics and computation, 177( 2 ): 807-818. https://doi.org/10.1016/j.amc.2005.11.092.

Li, Y., & Muldowney, J. S. (1993). On Bendixson′s criterion. Journal of Differential Equations, 106(1), 27-39.. https://doi.org/10.1006/ jdeq.1993.1097.

Li, M. Y., & Muldowney, J. S. (1996). A geometric approach to global-stability problems. SIAM Journal on Mathematical Analysis, 27(4), 1070-1083. https:// doi. org/10.1137/S0036141094266449.

Luenberger, D. G. (1979). Introduction to Dynamic System: Theory, Models and Applications,1sted.,John Wiley & Sons, NewYork. pp.336-38.

Aldila, M., & Aldila, D.(2018). Mathematical model for HIV spreads control program with ART treatment.In Journal of physics: Conference series, 9:012035. https://doi.org/10.1088/1742-6596/974/1/12035.

Munawwaroh, D. A., Heri, R., Khabibah, S. U. S., & Anindita, H. P. (2020, April). Analysis stability of HIV/AIDS epidemic model of different infection stage in closed community. InJournal of Physics: Conference Series.1524(1), 012130. https://doi.org/10.1088/1742-65 96/1524/1/012130.

Nath, B. J., Dehingia, K., Sadri, K., Sarmah, H. K., Hosseini, K., & Park, C. (2023). Optimal control of combined antiretroviral therapies in an HIV infection model with cure rate and fusion effect. International Journal of Biomathematics, 16(01), 2250062. https://doi.org/10.1142/S1793524522500620.

Ngina, P. M., Mbogo, R. W., & Luboobi, L. S. (2017). Mathematical modelling of in-vivo dynamics of HIV subject to the influence of the CD8+ T-cells. Applied Mathematics, 8(08), 1153. https://doi.org /10.4236/am.2017.88087.

Ngina, P., Mbogo, R. W., & Luboobi, L. S. (2018). Modelling Optimal Control of In‐Host HIV Dynamics Using Different Control Strategies. Computational and Mathematical Methods in Medicine, 2018(1), 9385080. https://doi.org/10.1155/2018/9385080.

Ogunlaran, O. M., & Oukouomi Noutchie, S. C. (2016). Mathematical model for an effective management of HIV infection. BioMed research international,2016(1), 4217548. http://dx.doi.org/10.1155/2016/ 4217548

Olabode, D., Rong, L., & Wang, X. (2019). Optimal control in HIV chemotherapy with termination viral load and latent reservoir. Mathematical Biosciences and Engineering, 16(2), 619-635. https://doi.org/10.3 934 /mbe.2019030.

Omondi, E. O., Mbogo, R. W., &Luboobi, L. S. (2019). A mathematical modelling study of HIV infection in two heterosexual age groups in Kenya. Infectious Disease Modelling, 4, 83-98. https://doi.org/10.1016/j.idm. 2019.04.003

Omondi, E. O., Mbogo, R. W., & Luboobi, L. S.(2022). A mathematical model of HIV transmission between commercial sex workers and injection drug users. Research in Mathematics, 9(1), 2082044. https://doi. org/10.1080/27684830.2022.208244.

Ouifki, R.,&Witten, G. (2007). A model of HIV-1 infection with HAART therapy and intracellular delays. Discrete and Continuous Dynamical Systems-B, 8(1),229-240. https://doi.org/10.3934/dcdsb.2007.8.229.

Pontryagin, L. S. (1986). Mathematical theory of optimal processes, 1sted.,Gordon and Breach Science, New York.Srivastava, P. K., Banerjee, M., & Chandra, P. (2009). Modeling the drug therapy for HIV infection. Journal of Biological Systems, 17(02), 213-223. https://doi.org/10.1142/S0218339009002764.

Sutimin, S., Sunarsih, S., & Tjahjana, R. (2018). Modeling CD4+ T-cells andCTLresponse in HIV-1 infection with antiretroviral therapy. Communication in Biomathematical Sciences, 1(2), 100-109. https://doi.org/10.56 14/cbms.2018.1.2.3.

Sutimin, S., Sunarsih, S., & Tjahjana, R. (2020). Modeling of HIV-1 infection incorporating cell-to-cell transmission and viral clearance of CD4+ T cells.In AIP Conference Proceedings, 2264, 020007. https://doi.org/10.1063/5.0024193.

Thahjana, H. (2019). Analysis of mathematical model of HIV-1 infection of CD4+ T cells with CTL response and antiretroviral treatment. InJournal of Physics: Conference Series, 1217, 012074. doi.org/10.1088/1742-6596/1217/1/012074

Tjahjana, R. H., & Sutimin, S. (2020). Optimal Control Approach For HIV-1 Infection in CD4+ T Cells with RTI and PI Treatments. International Journal of Computing Science and Applied Mathematics, 6(2), 42-45.

Van den Driessche, P., & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical biosciences, 180(1-2),29-48. https://doi.org /10.1016/S0025-5564(02)00108-6.

WHO. (2022). HIV.Retrieved February 9, 2023, from https://www.who.int/news-room/fact-sheets/detail/hiv-aids