The Performance of DEWMA and EWMA for ZIB Model when Underlying Distribution is the Ratio of Two Poisson Means

Direk Bualuang

The Performance of DEWMA and EWMA for ZIB Model when Underlying Distribution is the Ratio of Two Poisson Means

Authors

Direk Bualuang Department of Applied Mathematics, Faculty of Science and Technology, Uttaradit Rajabhat University, Thailand

Keywords:

Average Run Length, zero-inflated binomial, Markov Chain

Abstract

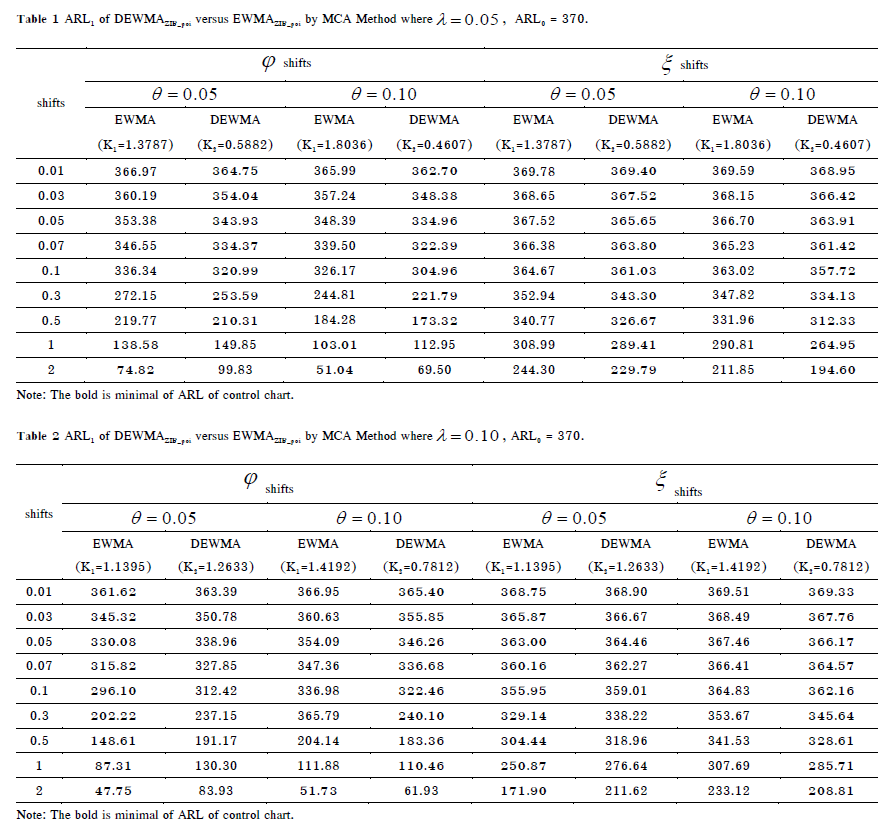
This research aims to present a double exponent weighted moving average (DEWMA) control chart for a Zero Inflated Binomial model under the ratio distribution of the two Poisson means (ZIBpoi) by the Markov Chain approach, this is also to compare the efficiency of DEWMA with EWMA procedure. The performance of DEWMA control chart gives an out-of-control signal quicker than EWMA control chart to small process shifts ( $gif.latex?\delta&space;\leq&space;1\sigma$ ) for $gif.latex?\varphi$ shifts and quicker than all cases for $gif.latex?\xi$ shifts.