Average Run Length of CUSUM Control Chart for SARX(P,1)L Model using Numerical Integral Equation Method

Abstract

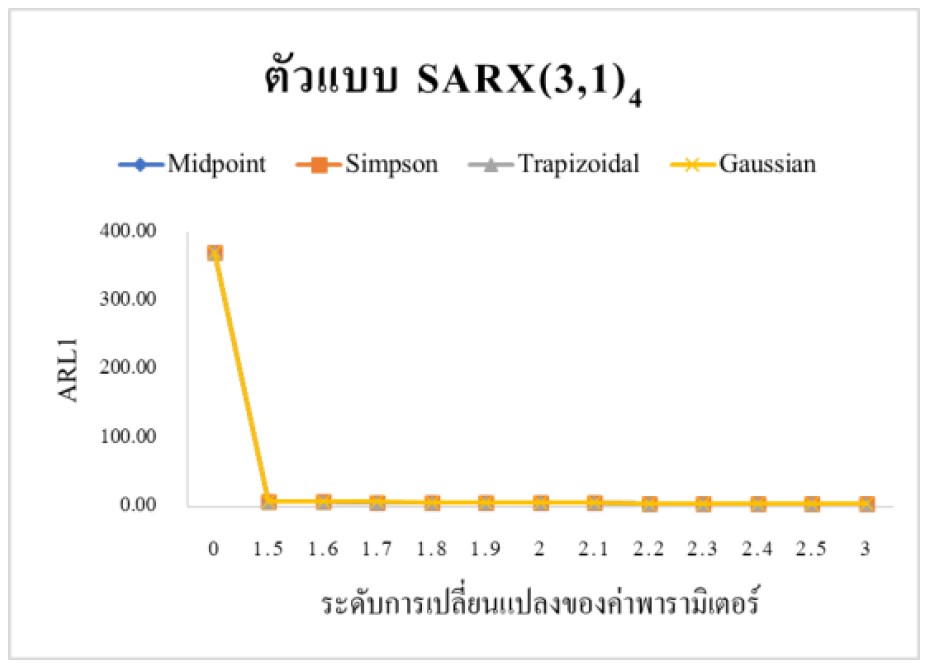
The main objective of this paper is to approximate the Average Run Length (ARL) of Cumulative Sum (CUSUM) control chart for a Seasonal Autoregressive with exogenous variable model; SARX(P,1)₄with Exponential white noise using the Numerical Integral Equation (NIE) method including Simpson rule, Midpoint rule, Trapezoidal rule and Gauss-Legendre Quadrature rule. The control chart’s performance are measured by Average Run Length (ARL) when the process is out of control by comparing the ARL values obtained from the four NIE methods and comparing the CPU Times. The results show that the ARL value obtained from the NIE methods by Simpson rule, Midpoint rule, Trapezoidal rule and Gaussian rule methods are not difference. While, the processing time by the Midpoint rule method was the lowest among the four methods.