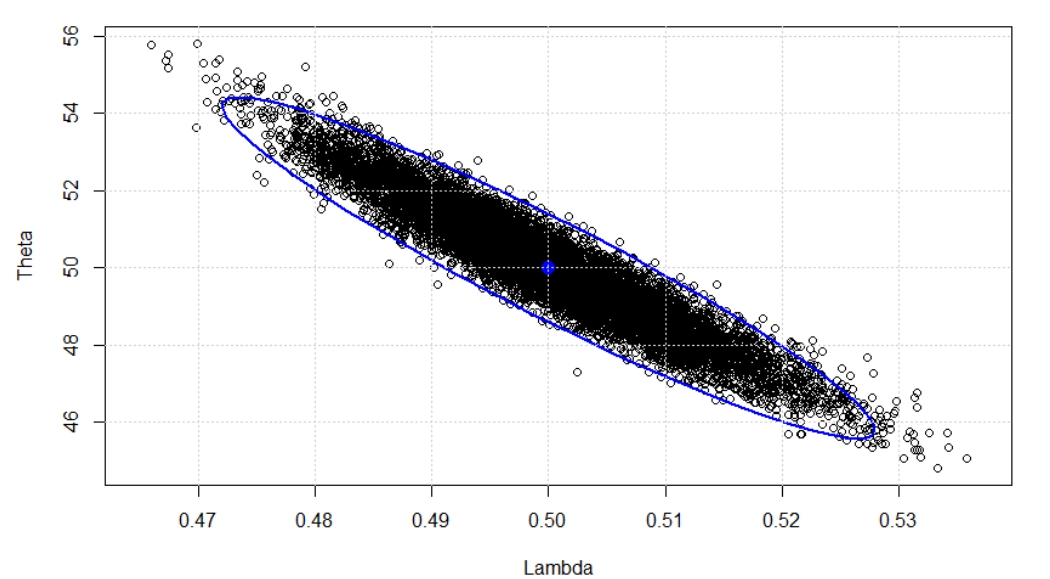
Asymptotic confidence ellipses for the re-parameterized inverse Gaussian distribution

Abstract

The re-parametrized inverse Gaussian distribution is a very useful distribution for statistics and it is applied to various fields, such as physics, engineering, biology, etc.  It is also appropriate to analyze the right-skewed data. In this research, we were interested in studying the Fisher-information matrix and we wanted to find the covariance matrix in order to form asymptotic confidence ellipses of parameters for the re-parametrized inverse Gaussian distribution. We compared the coverage probability with the confidence coefficient of 0.98 of confidence ellipses with sample sizes of  n= 10, 30, 50, 100, 1,000 and 10,000. The parameters of  lambda= 0.5, 1, 5, 10, 50 and  theta= 0.5, 1, 5, 10, 50.  The data were stimulated by Monte Carlo techniques which they were repeated 10,000 rounds in each model with RStudio programming.